Bridge to Quick Success in Mathematics for the ICSE. Chapter - Reminder Factor Theorem.
Problem types
I. To find the remainder of a given polynomial by actual division method and without division.
II. To prove that a devisor is a factor of the given polynomial. This is done by showing that the remainder equal to zero.
III. If there is a remainder the devisor is not a factor of the given polynomial expression.
IV. To find a single unknown constant, this may be the
coefficient of x3, x2 or x terms. These problems to find the
single unknown constant can be further can be subdivided.
a. A single polynomial with a single unknown constant and a factor without remainder or divisor with remainder.
b. Where the relationship between the two remainders is given.
i. A single polynomial with two divisors and their respective remainders.
a. When it is a factor the equation obtained after substituting f (x) in the given polynomial is equated to zero.
Equation 1 = 0
b. When the remainder is given, the equation obtained after substituting f (x) in the given polynomial is equated to the remainder.
Equation 2 = remainder.
ii. Two polynomials with a single divisor and their respective
remainders. R1 & R2
Equation 1 = R1
Equation 2 = R2
Solve with linear equations.
c. Where the relationship between the remainders and the unknown constant is given.
i. A single polynomial with two given divisors and their
respective remainders.
ii. Two polynomials with a single divisor and their respective
remainders.
V. To find two unknown constants using simultaneous equations.
a. A single polynomial with one factor given with no remainder
and one divisor given with a respective remainder is given.
Equation 1 (factor) = 0
Equation 2 (divisor) = R (remainder)
b. A single polynomial with two factors given.
Equation 1 (factor 1) = 0
Equation 2 (factor 2) = 0
c. A single polynomial with two unknown constants, two linear divisors and respective remainders is given.
Equation 1 = Remainder 1
Equation 2 = Remainder 2
d. A single polynomial with two unknown constants and two given factors.
Equation 1 (factor 1) = 0
Equation 2 (factor 2) = 0
e. A single polynomial with two unknown constants, a quadratic divisor and remainders is given.
f. Two polynomials with two unknown constants a single divisor and its respective remainders is given.
Equation 1 (polynomial 1) = Remainder 1
Equation 2 (polynomial 2) = Remainder 2
g. Two polynomial with two unknown constants and two linear divisors with their respective remainders is given.
Equation 1 (polynomial 1 & Divisor 1) = Remainder 1
Equation 2 (polynomial 2 & Divisor 2) = Remainder 2
h. Two polynomials with two unknown constants and a common factor is given.
VI. To completely factorise a given polynomial.
Type A –
a. We may be given a divisor and asked to prove it is a factor and
then completely factorise the given polynomial.
Type B -
b. We may be given an unknown single constant and told that a
divisor is a factor. We then have to find the unknown constant
and then substitute it in the given polynomial to get the complete
polynomial. Then we proceed to factorise completely.
Type C -
c. A factor is directly given and we use algebraic division to get a
quadratic quotient. The quadratic quotient is further factorised
by simple factorisation method to get two more factors.
Type D –
a. By trial and error method (inspection method) we have to find the
first factor.
In all the four subtypes (A to D) after finding the first factor, we have to use algebraic division to find a quadratic quotient. This quadratic quotient is further factorised to get two more factors by simple factorisation method.
VII. Finding a number that must be added or subtracted from a
given polynomial to make the resulting polynomial completely divisible
by a divisor or leaves a certain given remainder.
Solutions to all these problems
1. Write down the given single polynomial or the two given polynomials.
2. Write down equate divisor to zero and find the value of x.
3. Substitute f (x) in the given polynomial.
i. This may help you to find the remainder.
ii. This may help you to prove the given divisor is a factor, when the remainder is zero.
iii. It may help you form a linear equation to find the value of the single unknown constant
iv. It may help you form to simultaneous equations which must be solved to find the two unknown constants.
4. When we are asked to factorise completely use algebraic division to find the quotient which is a quadratic equation can further be factorised to find two additional factors.
5. When the term says completely factorised it means that all divisors are factors, therefore the remainder is zero. Therefore each factor is equated to zero.
6. In the case of two unknown constants if both the terms for the given polynomial are stated to be factors, then both equations are equated to zero.
Equation 1 = 0
Equation 2 = 0
7. If in the case of two unknown constants for a given polynomial if one term is a factor and the other term a divisor with a given remainder, then
Equation 1 = 0 (in the case of the factor)
Equation 2 = R (in the case of the remainder).
Take R to the other side to create a simultaneous equation.
Equation 2 – R = 0
8. In the case of two unknown constants where both given terms are divisors with respective remainders.
Equation 1 = R1
Equation 2 = R2.
Taking R1 & R2 to the LHS we get two simultaneous equations.
9. In the case of a one unknown constant, where we have a single polynomial with two divisors or two polynomials with a single divisor, both giving the same remainder then
Equation 1 = R
Equation 2 = R
Therefore, Equation 1 = Equation 2.
10. Steps for problems in general
Step 1 : Write the polynomial identity in descending order.
Step 2 : Equate the divisor to zero and find the value of x which will eliminate any unknown quotient.
Step 3 : Substitute the value of x in the given polynomial
Step 4 : Simplify to find the value.
i. If the remainder is zero the divisor is a factor.
ii. If there is a remainder the divisor is not a factor.
iii. If it is given that the divisor is a factor, equate the value obtained by substituting f (x) in the given polynomial to zero.
iv. If a remainder is given and we are asked to find the unknown constant equate the value obtained by substituting f (x) in the given polynomial to the remainder.
Step 5 : If the remainder is zero then the divisor will be a factor of the given polynomial.
Step 6 : If the divisor leaves the remainder is not a factor for the given polynomial.
Step 7 : Solve linear, simultaneous equations as required.
Key points for solving problems with unknown constant.
(i) Decide whether there are one unknown (linear equation) or two unknown (simultaneous) constants.
(ii) Decide whether there is one or two given polynomial expressions.
(iii) Decide what is given.
a. Two factors
b. one factor and one divisor with remainder.
c. Two divisors with respective remainders. (R1 & R2)
Key points for solving problems when a polynomial expression is given but no factors are given.
i. This is known as Trial & Error Method or Inspection Method.
ii. Take x = 1, and substitute in the polynomial expression. If the remainder is zero (x – 1) is a factor.
x = 1 , x – 1 = 0, (x – 1) is a factor.
iii. If we don’t get a remainder zero then try and substitute
x = - 1 in the polynomial expression. if a remainder is zero is obtain then x = - 1 is a factor. x + 1 = 0 is a factor.
iv. If you are unsuccessful with 1 and – 1 to get a remainder of zero then try with x = 2, then (x – 2) is a factor and x = - 2, then (x + 2) is a factor, if the remainder is zero.
v. Similarly try with x = 3 and x = - 3, if unsuccessful with +2 & - 2.
vi. Keep substituting till you get a remainder of zero for a given number.
vii. So the order of trial with numbers is (+1, - 1, +2, - 2, +3, - 3) being substituted in the given polynomial expression to get the remainder of zero.
Problems on Remainder Theorem
1.Find the remainder (without division) when
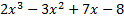
Problem type – Single polynomial with single divisor. Ask to find the remainder.
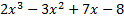 |
Step 1: Write the polynomial identity in descending order |
x – 1 = 0
x = 1
f(x) = f (1)
|
Step 2 : Equate the divisor to zero and find the value of x which will eliminate any unknown quotient. |
2(1)3 – 3(1)2 + 7(1) – 8
f (1) = 2 – 3 + 7 – 8
f (1) = 9 – 11 = -2.
|
Step 3 : Substitute the value of x in the given polynomial |
Remainder = -2
∴ (x – 1) is not factor for polynomial.
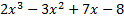 = 0 = 0
|
Step 4: If there is a remainder the divisor is not a factor. |
Given,
i. (Polynomial ) Dividend = 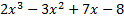
ii. Divisor = (x-1)
iii. Coefficient = x3 = 2
= x2 = -3
= x = 7
Constant = - 8
Ask to find the Remainder.
2. is divided by (x+1), the remainder is 2.
is divided by (x+1), the remainder is 2.
Find the value of constant k
Problem type – single polynomial expression with single divisor with remainder given. To find the value of a single unknown constant.
 |
Step (1): Write the polynomial identity in descending order |
x + 1 = 0
x = 1 |
Step (2): Equate divisor to zero and find the value of x, determine the unknown |
 = 2 = 2 |
Step (3): Equate the polynomial to the given remainder. |
k(-1)3-9x2+4x-10=2
-k+9-4-10= 2
k-5 = 2
-k = 2 + 5
-k= 7
k=-7 |
Step (4): Substitute f(x) |
k=-7 |
Step (5) A single polynomial with an unknown constant and a divisor with a remainder given. |
3. When divided by x – 3, the polynomials x3-px2+x+10 and
2x3-x2-(p+3)x-6 leave the same remainder. Find the value of 'p'.
Problem type single polynomial expression with single divisor with given remainder. To find single unknown constant.
x-px2+x+10 |
2x3-x2-(p+3)x-6 |
Step 1 : Write down the given polynomials |
x – 3 = 0
x = 3 |
x – 3 = 0
x = 3 |
Step 2 : Equate the given divisor to zero and obtained the value of x |
(3)3 – p(3)2 + 3 + 6
27 – 9p + 3 + 6
36 – 9p |
2(3)3-32-(p+3)-6
54 – 9 – 3p – 9 – 6
54 – 24 – 3p |
Step 3 ; substitute f (x) = f (3) in the given polynomial. |
| 36 – 9p = R
Equation 1 |
30 – 3p = R
Equation 2 |
Step 3 : Equate the polynomial to the given same remainder |
Equation 1 = Equation 2 (remainder is same)
36 – 9p = 30 – 3p
36 – 30 = 9p – 3 p
6p = 6
P = 1 |
Eqn. 1 = Eqn. = 2
Solving the linear equation and find the value for p. |
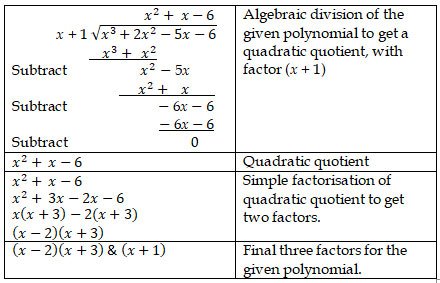
4. (i) Show that (x – 3) is a factor of x3-7x2+15x-9. Hence
factorise x3-7x2+15x-9.
Problem sub type : A single polynomial is given. A divisor is given that must be proven to be a factor (remainder = 0)
Then we are ask to factorise the polynomial completely.
x3-7x2+15x-9 |
Step (1): Write the polynomial identity in descending order. |
(x – 3)
x = 3 |
Step 2 : Equate the given divisor to zero and obtain the value of x. |
(3)3-7(3)2+15(3)-9
= 27 – 63 + 45 – 9
= 72 – 72
= 0 |
Step 3 : substitute f (x) = f (3) in the given polynomial. |
(x – 3) is a factor. |
The remainder is zero. |
x2-4x+3 |
Algebraic division of |

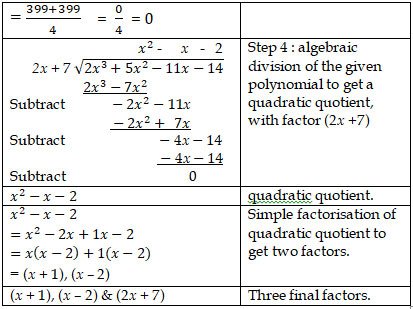
5. Show that (2x + 7) is a factor of 2x3+5x2-11x-14. Hence, factorise the given expression completely using factor theorem.
Problem sub type : A single polynomial is given. A divisor is given that must be proven to be a factor (remainder = 0)
Then we are ask to factorise the polynomial completely.

6. Find the value of a if (x – a) is a factor of x3-ax2+x+2
Problem sub type : A single polynomial is given. A factor is given. To find the single unknown constant.

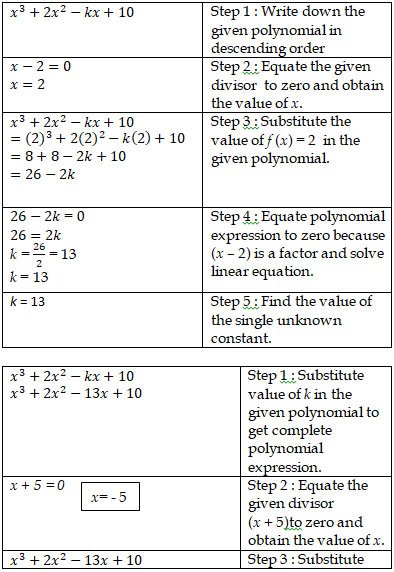
7. Find the value of k, if (x – 2) is a factor of x3+2x2-kx+10.
Hence determine whether (x + 5) is also a factor. Factorise
completely.
Problem sub type : A single polynomial is given. A factor is given. To find the single unknown constant. Then we are asked to factorise completely.

8. If (x – 2) is a factor of 2x3-x2-px-2
(i) find the value of p, (ii) with this value of p, factorise the above expression completely.
Problem sub type: A single polynomial is given. A factor is given. To find the single unknown constant. Then we are asked to factorise completely.


9. Use factor theorem to factorise the polynomial completely.
x3-3x2-10x+24
Problem sub type : A single polynomial is given. Then we are asked to factorise completely. No factor is given. (Trial & Error method / inspection method)

(ii) Use factor theorem to factorise the polynomial completely.
x3+ x2-4x- 4


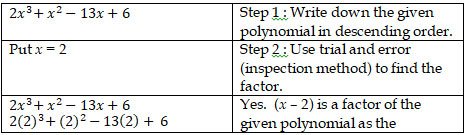
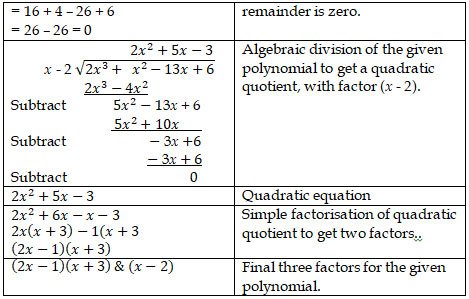
10. (i) Use the Remainder Theorem to factorise the following
expressions : 2x3+ x2-13x+6.
Problem sub type : A single polynomial is given. Then we are asked to factorise completely. No factor is given. (Trial & Error method / inspection method)
(ii) Use remainder theorem, factorise completely :
3x3+2x2-19x+6
Problem sub type : A single polynomial is given. Then we are asked to factorise completely. No factor is given. (Trial & Error method / inspection method)

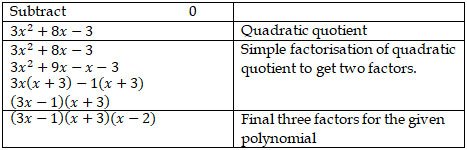
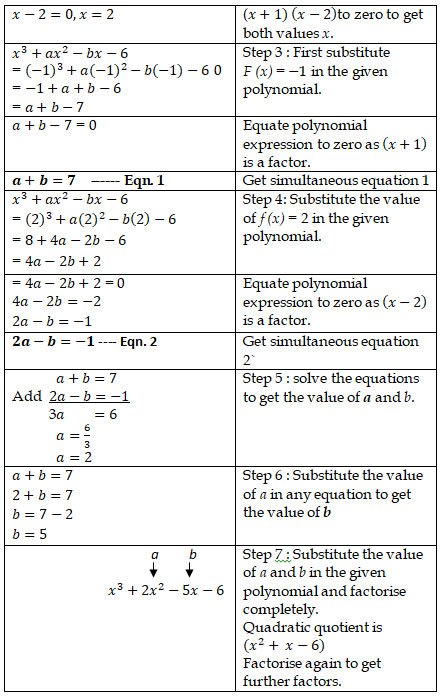
11. Find the values of the constants a and b if (x-2) and (x+3) are
both factors of the expression : x3+ax2+bx-12
Problem sub type : A single polynomial is given. Two factors are given. We are ask to find two unknown constants (simultaneous equation)


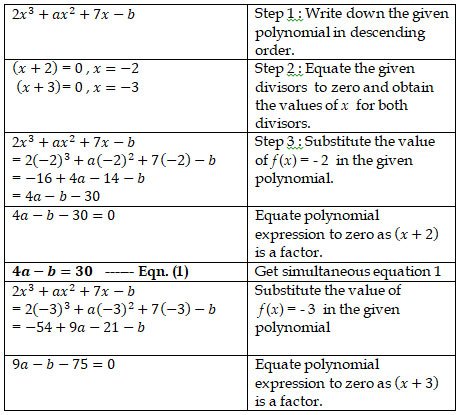
12. Given that x+2 and x+3 are factors of 2x3+ax2+7x-b.
Problem sub type : A single polynomial is given. Two factors are given. Then we are asked to find the value of the two unknown constants.

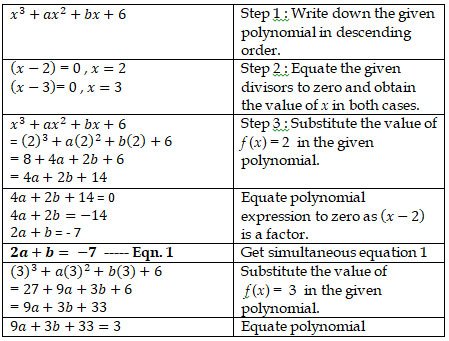
13. If (x - 2) is a factor of the expression x3+ax2+bx+6, when
this expression is divided by (x – 3) it leaves the remainder 3.
Find the value of a and b.
Problem sub type : A single polynomial is given. A single factor
(x – 2)is given. A single divisor (x – 3) with remainder is given. Then we are asked to find the values of two unknown constants.

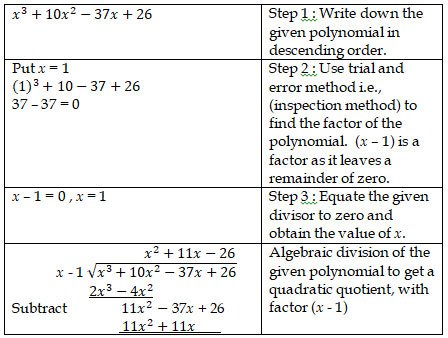
14. Using the Remainder and Factor Theorem, factorise the
following polynomial : x3+10x2-37x+26
Problem sub type : A single polynomial is given. Then we are asked to factorise completely. No factor is given. (Trial & Error method / inspection method)

15. If (x + 3) & (x – 4) are factors of x3+ax2-bx+24, find the
value of a and b with these values of a and b factorise the given
expression.
Problem sub type: A single polynomial is given. We are given two factors. We are asked to find the value of two unknown constants. Then we are asked to factorise completely.


16. Given that (x+1) and (x-2) are factors of x3+ax2-bx-6,
find the value of a and b and factorise the given expression
completely.
Problem sub type : A single polynomial identity is given. Two factors are given. We are asked to find two unknown constants. Then we are asked to factorise completely.

17. If (2x + 1) is a factor of both the expressions 2x2-5x+p and
2x2+5x+q, find the value of p and q. Hence find the other
factors of both polynomial.
Problem sub type : Two polynomials are given. A single common factor is given. We are asked to find the value of two unknown constants. Then we are asked to factorise completely.


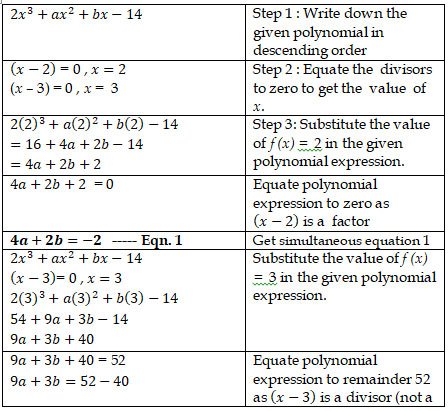
18. If 2x3+ax2-11x+b leaves remainders 0 and 42 when divided
by (x – 2) and (x – 3) respectively, find the values of a and b.
With these values of a and b, factorise the given expression.
Problem sub type : A single polynomial is given. Two divisors are given. Their respective remainders are given. Then we are asked to factorise completely.


19.If 2x3+ax2+bx-2 has a factor (x+2) and leaves the
remainder 7 when divided by (2x-3). Find the value of a and
b with these values of a and b factorise the given polynomial
completely.
Problem sub type : A single polynomial is given. We are given one factor. We are given a divisor with remainder. Then we are asked to find two unknown constants. Then we are asked to factorise completely.



20. Give f (x) = ax2+bx+2 and g(x) = bx2+ax+1, if (x – 2) is a
factor of f (x) but leaves the remainder – 15 when it divides g(x).
Find the value of a and b, factorise the expression
f (x) + g (x) + 4x2+7x.
Problem sub type : We are given two polynomial expressions. We are given a single divisor which is a factor for the first polynomial but is a divisor with a remainder for the second polynomial. Then we are asked to find the value of both unknown constants. Then we are asked to factorise completely.



21. If (x - 2) is a factor of the expression 2x3+ax2+bx-14, and
when the expression is divided by (x – 3) it leaves the remainder
52. Find the value of a and b.
Problem sub type : A single polynomial is given. We are given one factor and one divisor with remainder. Then we are asked to find the value of both unknown constants. Then we are asked to factorise completely.

22. Show that (x-1) if a factor of x3-7x2+14x-8. Hence
completely factorise the above expression.
23. Find the value of the constants a and b, if (x – 2) and (x + 3) are
both factors of the expression x3+ax2+bx-12.
24. Find the remainders when 2x3-3x2+7x-8 is divided by
x – 1.
25. Using factor theorem, show that (x – 3) is a factor of
x3-7x2+15x-9. Hence, factorise the given expression
completely.
26. Find the value of a, if (x – a) is a factor of x3-a2x+x+2.













































